Approximating simple functions with MLP networks

The universal approximation theorem and you

I have lately been thinking about the universal approximation theorem and in particular, how it plays out in practice.

For those who do not know, the universal approximation theorem states, roughly speaking, that a wide enough feed-forward network can implement an arbitrarily close approximation of any given function.

This means that if we take a function, no matter how complex, we can build an MLP network¹ to essentially compute this function to arbitrary levels of precision - only capped by how wide we are willing to make it.

While that is in principle encouraging, the myriad of practical issues encountered when training these types of networks to learn somewhat complicated functions suggests that as far as practice is concerned, there are many important considerations that are glossed over from this point of view.

So I got curious: How wide is “wide enough” as it relates to certain types of (relatively simple) functions? How much precision can be expected? How often do approximations learned via gradient descent behave well when going out of distribution?

The approach

In order to make some progress on these questions, a simple test harness can be built. This test harness will consist of the following elements:

1. A function to approximate

2. A sample input distribution to learn the approximation from

   1. Essentially, we just take samples from our input and do supervised learning with x as input and f(x) as the learning target, using MSE loss to optimize the network

3. A simple feed-forward MLP with a single hidden layer, a batch norm and ReLU activation²

4. An optimizer to train the network until we can be reasonably sure that it has converged

5. An evaluation harness that checks how well the trained network performs

The functions

The next question is which functions to test. Mostly for simplicity and ease of mental framing, I chose the following:

\(\begin{align} f(x)&=x^2\\ f(x)&=\sqrt{x}\\ f(x)&=|x|\\ f(x)&=\sin(x)\\ f(x)&=\log(x)\\ f(x)&=e^x \end{align}\)

The process

In order to get a decent sense for how well networks are capable of approximating each of these functions, I vary the size of the hidden layer from 1 to 128 - the more hidden parameters it has, the better the approximation it should produce, plus we can get a sense for how “difficult” it is for the network to fit any given function by evaluating how many hidden parameters are necessary to get to a decent approximation.

Since the goal is to be able to quantify this, I am tracking the following measures for each trained network:

• Cumulative L1 loss³ on 5 randomly sampled training batches

• Cumulative MAPE⁴ on 5 randomly sampled training batches

• Cumulative L1 loss on an evaluation domain

• Cumulative MAPE loss on an evaluation domain

The evaluation domain is generally chosen twice as large as the training distribution, that is, if the network is trained using inputs from [-1, 1], the evaluation domain is [-2, 2]. The goal is to get a sense for how the approximation behaves once it goes out of distribution.⁵

In addition to this, I am a primarily eyesight driven hairless ape, therefore I also generated some graphs as well.

The results

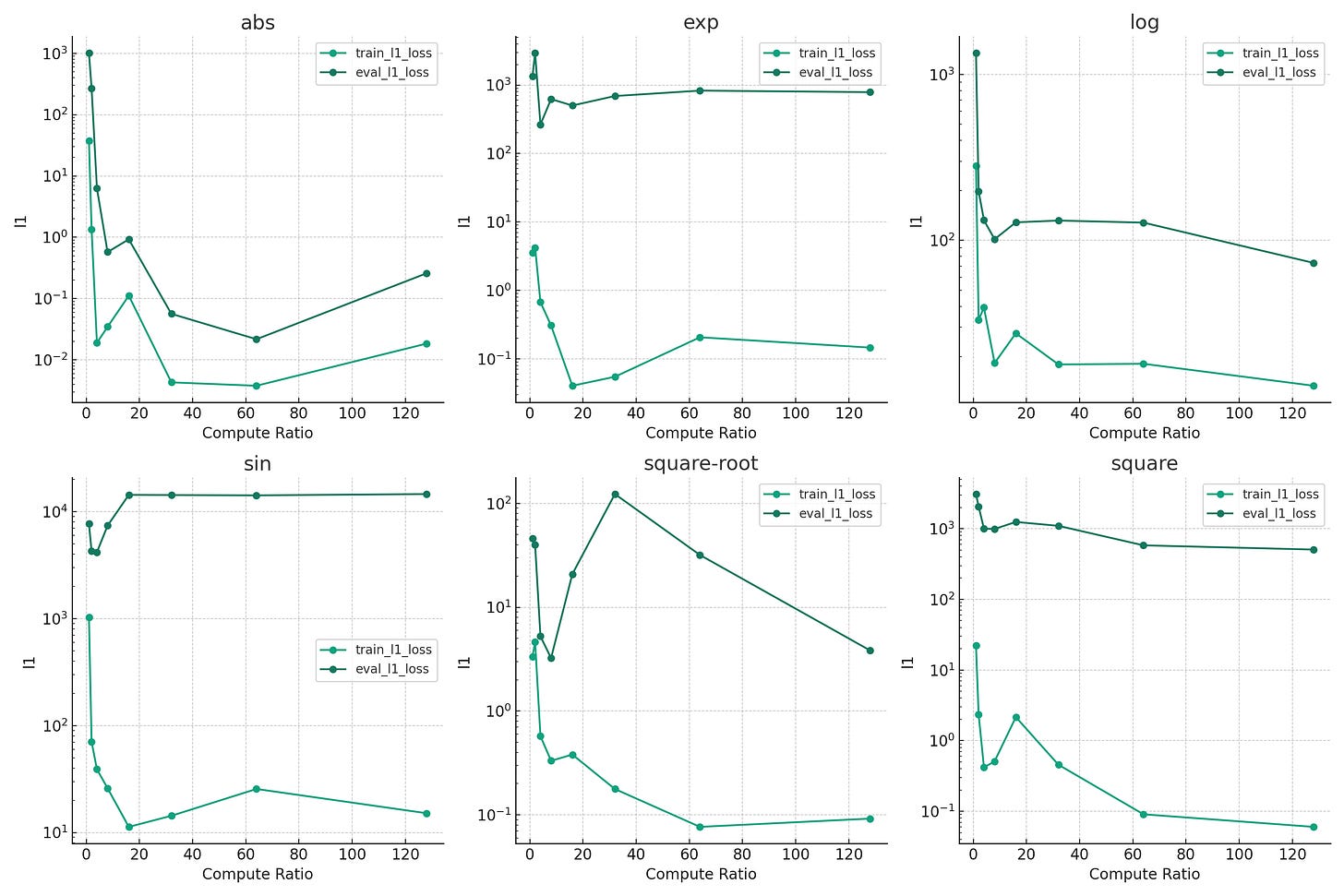
The below chart details the cumulative L1 loss (evaluated as described above) as a function of the size of the hidden layer for each of the functions tested. I made the y-axis logarithmic for easier viewing, as the differences can be fairly large. Note that only the highlighted points mark actual data samples taken, so the underlying behaviour may be a lot less smooth than implied.

This chart is the same as the above, except it details the cumulative MAPE loss instead of the L1 loss - the y-axis is logarithmic here, too.

Some observations I found interesting

• For each of the modelled functions, there is very clearly a cut-off point where adding additional hidden parameters does not significantly improve either evaluation or training performance

• A lot of functions require in the range of 8 to 32 hidden parameters for the network to be able to build a compelling approximation

• Periodic functions are the bane of ReLU-based MLP networks the moment you go out of distribution and adding more hidden parameters does not seem to fix this

For fun, I have created a video showcasing how the approximation vs real function evolves as the network is afforded a larger hidden layer. Each plot is titled “<function_name>_r<hidden_size>” - so “abs_r001” (the first top-left plot) is for trying to approximate the abs function with a hidden layer of size 1. Each plot shows the true underlying function in blue, the networks approximation in orange and the L1 loss in green.

Conclusion

After having done all this I have learned some things. Not necessarily all the things I was thinking to learn, but learning tends to always be good.

It seems fairly straightforward now why ReLU-based or ReLU-like activation functions work really well and are quite robust: They simply continue with a decent-ish approximation of the slope near the edges of the training distribution when going out of distribution (the plots in the above video for the square function are especially telling). This means that especially for modeling functions whose underlying gradient changes slowly, their OOD behaviour is very stable and useful and often still quite close to the true function.

This also means that the OOD behaviour of ReLU-based activations will likely be absolutely terrible if the underlying function being modelled is discontinuous - something to test for another day (for example, testing f(x)=round(x*10)/10 or similar functions).

Additionally, I find the framing of these networks as essentially assembling tiny piecewise versions of the activation function in order to build their approximation as fairly helpful in understanding how the approximation itself comes about - ReLU makes this behaviour very straightforwardly apparent, though I do not expect this to be a technically accurate description of the underlying phenomenon for all possible activation functions.

It is also noteworthy that for an MLP model to be able to do meaningful computation on any given input parameter, there should be somewhere in the range of 8 to 32 hidden parameters present for this input parameter. Naturally, this property applies no matter where in a larger NN setup you are - if you require an MLP model to learn some nontrivial transformation of its input, it likely pays to make the hidden layers quite a bit larger than the input.

I think a lot of these results do not transfer easily to predicting the dynamics and behaviour of multi-layer networks, but that too is something to think about and try to figure out later.

All in all, I am quite happy with this little experiment and what it has taught me - hopefully you thought so, too.

1. Incase you are unfamiliar, here is a videoseries with the best explanation of the basic idea I have encountered so far.

2. relu(x) = max(0, x) - or check wikipedia for some additional context - it is a really simple function at its core.

3. The L1 loss is the sum of the absolute differences between the predictions and the correct values. If you need more technical detail, you can check out the pytorch documentation.

4. MAPE is short for “Mean absolute percentage error” - pretty much literally what its name implies. Take the absolute difference, then divide by the absolute value of the correct value. “Cumulative” means instead of taking the mean, I sum up all individual absolute percentage errors. If you need more technical detail, wikipedia can help.

5. If you need all the details about how this data was generated, you can check out the companion repo to this post.